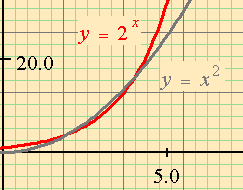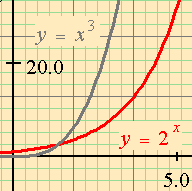|
MathXpert: Learning Mathematics in the 21st Century Michael Beeson ABSTRACT: MathXpert is a computer program designed to help students learn algebra, trigonometry, and one-variable calculus. Its scope extends from elementary algebraic manipulations to the most complicated limits and integrals usually considered in University classes. It is capable of generating complete, step-by-step solutions to mathematical problems, but normally this capability is used to assist the student in developing his or her own step-by-step solution. The design of MathXpert follows principles dictated by its intended use to support learning; these principles and how they influenced MathXpert are discussed. The paper concludes with a discussion of the current and future use of technology in general, and MathXpert in particular, in mathematics education. KEY WORDS: mathematics education, computer algebra, calculus 1. IntroductionMathXpert is a system that allows a person to do mathematics on a computer screen in much the same way as it is done with pencil and paper, but with some important differences: (1) It is not possible to make a mistake. (2) If you do not know what to do, MathXpert can help you. These features of MathXpert should be compared to the two main difficulties that people experience in their attempts to learn mathematics:
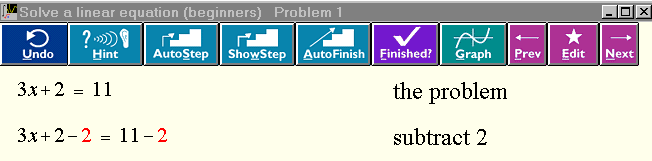
Maria Montessori, the Italian educator, introduced the idea that educational materials ought to be self-correcting [MON 17, pp. 74-75]. That means that the student should be able to discern, by the design of the exercise itself, when the work has been correctly completed, without appeal to authority. She designed many physical materials for young children with this principle in mind. But in the usual means of teaching algebra and calculus, appeal to authority is the usual way in which students verify the correctness of their work--for example, by checking the answer in the back of the book. Worse, there may be no error correction at all . Often, students make a mistake at the third line of a solution, but are unaware of it, and expend a lot of time and energy on work which is completely useless. Worse, they may not be able to find their own mistake. This leads to frustration and, if it is often repeated, to a feeling of failure and so-called "math phobia". MathXpert is designed to provide a self-correcting way to learn mathematics. For example, suppose you think (incorrectly) that ln(x+y) = ln x + ln y. You will not be able to apply this incorrect rule in MathXpert, because only correct rules are offered as menu choices for you to choose. If you have in mind to use this incorrect rule, you will learn something from its unavailability. You may, of course, have to ask your teacher why it isn't there. MathXpert is meant to replace blackboards and homework (and graphing calculators), but not teachers and books. (I do not believe that it is even desirable to replace teachers and books by computers--see the section on societal implications later in the paper.) 2. Transparency: MathXpert shows all the steps The first and most important design principle of MathXpert is the "glass box" or "transparency" principle--show all the steps. Indeed, this principle combines with the idea that the user should be in control to dictate the basic design of MathXpert: the user chooses the steps and thus controls the development of the computation, while the computer carries out the low-level details. I will give two examples of the use of MathXpert, one from beginning algebra, and one from second-semester calculus, showing how this works out in practice. 2.1. Carry out a calculation with MathXpert Let us begin by pretending it is the first day of algebra class. The student is learning how to solve simple linear equations such as 3x + 2 = 11. After entering the problem (or selecting it from the problems that come with MathXpert), the user reaches the working screen, and sees this:
Ignoring the buttons for now, and supposing that we know how to work this problem on paper, let us see how to use MathXpert. We want to subtract 2 from both sides of the equation. So we use the mouse to select the 2, just as you would select some text in a word processor:
As soon as you release the mouse button you will see a popup menu of operations that can be carried out with or to the selected expression:
In the menu, the question mark stands for the selected expression. We see the operation we want, Subtract ? from both sides. Choosing that operation yields the next line of the solution:
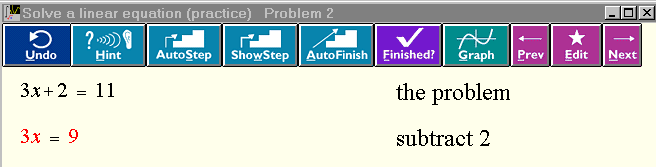
The "-2" is shown in red, indicating the changed parts of the equation. We entered this problem under the topic "linear equations (beginners)". If we had chosen "linear equations (practice)" instead, the result of the operation would have been this:
This shows how MathXpert can produce more detailed or less detailed output depending on the level of the student. On the first day of learning linear equations, the student really needs to see 3x+2-2, but subsequently that would be annoying. Continuing in this fashion, one generates in a few more steps the complete solution:
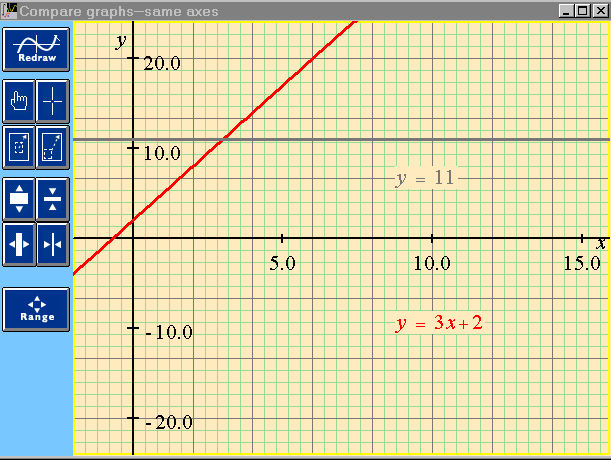
It would not have been possible, for example, to subtract 2 from one side of the equation and not from the other. On the other hand, any operation which is mathematically legal can be carried out. For instance, we could at the first step add 2 to both sides, or write 11 as 5 + 6, or divide the entire equation by 3 without subtracting 2 first, etc. 2.2 Never more than one click from a graph Clicking the Graph button we see the solution of the linear equation graphically:
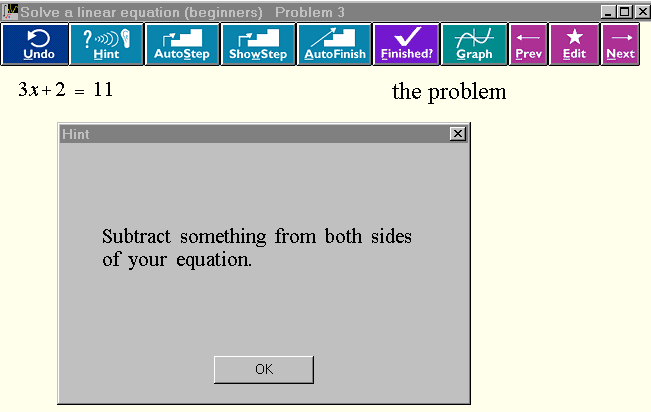
The diagonal line is red and represents y = 3x + 2. The horizontal line is grey and represents y = 11. The formulas are printed in matching colors. The solution is found at the intersection of the two lines. The Point-Slope tool can be selected by one of the buttons at the left and used to see the numerical coordinates of the point of intersection (this is not shown here). 2.3 MathXpert provides hints or help carrying out steps when requested MathXpert can use its ability to solve mathematical problem in several different ways to advise the student. Let us imagine that, as a beginning algebra student, we are staring at the statement of the problem above, and we have no idea how to proceed. So, we click the Hint button. We receive advice which is clear and to the point:
Let us suppose that for some reason we are not able to understand and follow this advice. We can then click the ShowStep button. The cursor will then move by itself to illustrate how we should select the "2"; the popup menu of possible operations will appear, the cursor will move to the correct choice, and it will be highlighted, but not actually applied. The user will only have to read the menu and click on the selected item to advance to the next solution step. Simply advancing to the next solution step can be done immediately with the AutoStep button. This can be useful for making MathXpert carry out one or more completely routine and well-understood steps quickly. But ShowStep not only shows the result of the next step, it shows what operation should be applied to achieve it, and what term should be selected to carry it out. The AutoFinish button causes MathXpert to complete the entire solution, however many lines it requires. Each step is shown, with its justification. Some teachers have expressed a fear that students would just press AutoFinish on each problem to be done with their homework as quickly as possible. This is almost never the case. Students enjoy developing their own solutions and take pride in them. If anything, they make too little use of AutoStep. Note that AutoFinish proceeds from whatever point has already been reached--it does not start over. The solution generated by AutoFinish starting from the original problem is called the "automode solution". While MathXpert does generate a unique automode solution for each problem, it still supports "multiple solution paths", in that a student can develop any correct solution. Often there is more than one correct way to solve a problem. Sometimes it is enough to take the first step of an alternate solution, after which AutoFinish will complete the alternate solution instead of the one it would have generated from the original problem. In accordance with the principle that the user is in control, MathXpert never "intervenes" to provide help. The user is free to "wander" by taking any mathematically correct steps at all, whether or not they are leading towards an "ideal" solution of the problem. Having reached an awkward solution, the user may choose to compare it with MathXpert's automatic solution--but that would be the user's choice. At no point will an avuncular voice tell the student to do something different. 2.4 An example in calculus We have seen that MathXpert can give detailed advice to a beginner in algebra. Now we will see that MathXpert's internal abilities extend to advanced integration techniques:
Note that the decomposition into partial fractions was carried out in one step. The algebraic manipulations necessary to find the partial fraction decomposition are a distraction when the student is learning integration techniques. Here is a good place for the computer to carry out the details. That is, we have a "black box" operation used at a low level in the "glass box" solution (showing all steps) of the integration problem. 2.5 Scope of MathXpert: three years of mathematics MathXpert offers comprehensive support for all the topics of beginning, intermediate, and advanced algebra, trigonometry, exponential and logarithmic functions, sigma notation, complex numbers (including complex quadratic equations, polar form, de Moivre's theorem), beginning calculus including "differentiate from the definition of derivative", evaluation of limits, integration by substitution and parts. Calculus 2 includes all standard integration techniques, including partial fractions, trigonometric substitutions, etc. Graphical solution of differential equation is included but not symbolic solution. Infinite series are not supported in the commercially-available version of MathXpert. 3. MathXpert's computer algebra is correct One of the principles of MathXpert is that you can never derive an incorrect answer. Many people tend to take it for granted that computers would never make a mistake in algebra, but in fact this "correctness principle" is violated by all other computer algebra systems, and it was difficult to program MathXpert to comply with it. For example, in most other computer algebra systems, you can start with the equation b= 0, and divide both sides by b. On the left you will get b/b = 1, and on the right you will get 0/b = 0. Thus you have derived the wrong equation 1=0. The problem here is that the other systems do not keep track of the assumptions and the side conditions. Most of the time in mathematics, the validity of the current equation depends on certain assumptions, and the applicability of a mathematical operation (such as dividing both sides by b) depends on the truth of certain side conditions (such as b not being zero). To carry out the operation correctly, the truth of the side conditions must follow from the current assumptions. In the example, that certainly is not the case. The side condition that b should be nonzero is in fact contrary to the first line, b = 0. If you try this in MathXpert, you will get a message that you cannot divide by zero, and the operation will be blocked. The side conditions of operations can be quite complicated. For example, if we try to integrate 1/x from -1 to 1, many computer algebra systems will simply form the indefinite integral 1/|x| and evaluate it from -1 to 1, producing the answer zero, failing to note that the integral is undefined due to the singularity at zero. The side condition that the function should be continuous on the (closed) interval of integration is not checked. One may hope that scientists and engineers will be able to judge the correctness of answers they receive from computer algebra systems. Whatever one thinks about that, clearly wrong answers from a program will be unacceptable in education. To make MathXpert satisfy the correctness principle, I had to build a program to keep track of assumptions and side conditions, and be able to infer side conditions from assumptions. Such a logical program belongs to area of research known as "automated deduction", in which the aim is to get the computer to make logical deductions automatically. This part of MathXpert, its "prover", was one of the most difficult parts to program. It functions almost invisibly, since in education it is not customary to show the assumptions explicitly. In MathXpert, the assumptions can be viewed at any time by choosing Affichage | Hypothèsis from the menus. What happens if the prover cannot infer the side condition of the user's chosen operation? Consider the operation
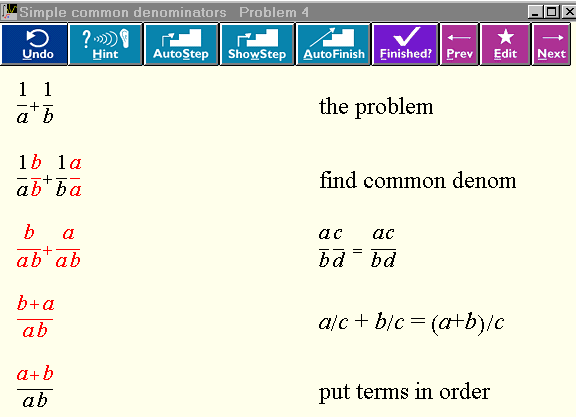
The side condition is x³ 0. If we try to apply this operation with x=2, it will work, because the prover is able to infer that 2 is positive. If we try it with x = -2, it wil not work, because the prover is able to refute the side condition. If we try it with a variable for x, it will work (in some types of problems), but the side condition will become a new assumption. That is, x³0 will be assumed. On the other hand, if we are solving an equation for x, this is not appropriate, as we will lose any negative solutions. But if the variable is just a parameter in the equation, then it is good to make assumptions as required. For example, we want to solve ax = 1 for x, getting x = 1/a, and generating the assumption that a is not zero. More details about the connections between logic and computation in MathXpert can be found in [BEES 92]. 4. MathXpert as teacher Although MathXpert is meant to replace blackboards and homework, but not teachers and books, nevertheless it does supply information (like books) and help (like teachers) in some ways. We have seen that it is able to use its symbolic calculation "engine" to provide hints, to provide the next step (or all the steps), and to "show the next step", complete with term selection and menu choice. Also, the steps that MathXpert takes can be different, depending on the student's knowledge of mathematics. For beginners, MathXpert provides many small, thoroughly explained steps. For non-beginners, this would be annoying, and MathXpert provides steps of an appropriate difficulty or "grain size". In this section we discuss the principles that govern these parts of MathXpert's design. 4.1 The user remains in control MathXpert never attempts to control the interaction with the user--it always responds to user requests. It does not attempt to "intervene" when their model of the user's behavior indicates that the user is lost, or not following a good solution path. MathXpert allows the user to take any mathematically legal step, whether it is "productive" or "goal-oriented" or not. It does not evaluate the user's work at any intermediate stage. Only when the user requests evaluation by pressing the Terminé button, or when the user explicitly requests a hint, or to be shown the next step, does MathXpert evaluate the work. It does not monitor whether the user is following some ideal "solution path" or inventing a new and creative solution path, or is completely lost. In this respect, MathXpert is in the mainstream of intelligent tutoring programs, according to [A-K 00], who state that the system should let students control and organize their own learning processes; the system should intervene as little as possible, and help should be given on request only. The underlying assumption is that the student herself is a better judge of when help is needed that the system, which does not have much bandwidth to access a student's thoughts, and may not have a complete enough domain model to account for all observed strategies. The paper from which this quotation is taken goes on to describe evidence that in one particular tutor, the students often wait too long before requesting a hint, in the sense that they have already made multiple errors. This carefully researched observation is consistent with my informal observations of students using MathXpert. The quoted authors attribute this to the students' poor "metacognitive skills"--that is, they just don't know that they need help when they have made multiple errors. I would like to suggest another interpretation: the students simply have a strong desire to complete the problem themselves, to succeed without help. Even though they have made multiple errors, they show their courage and determination by continuing on against the odds, until finally desperation drives them to seek help. A clear understanding of these matters may enable us to improve software design, not only of MathXpert but of other tutors as well. While this point is interesting, it is not vital, as several useless steps can be tried quickly and undone, and no step can be taken which is actually incorrect, so even the most determinedly independent student cannot go completely off the track before giving up and asking for help. 4.2 Instruction is tailored to the student's level It has long been one of the aims of applied artificial intelligence to provide "intelligent tutors". These would be computer programs which maintain internal models both of the student and of the subject matter, and use these models to control their interaction with the student. When I first read about the work of J.S. Brown and others in modelling students' misconceptions, I was extremely impressed, and intended to build a "user model" into MathXpert. Indeed, MathXpert still contains a "user model" of sorts. This consists in recording, for each of some 1600 mathematical operations, whether that operation is at the moment well-known, known, learning, or unknown. It is this user model that controls the level of detail shown in the automode solution. For example, in the linear-equations example in the introduction, when adding something to both sides is learning, it does not simplify the result, but when it is known or well-known, it does simplify the result. Thus we got 11-2 in the first case and 9 in the second case. If this problem were entered under an advanced-algebra topic, it might have been solved in one step with the justification Solve linear equation. That one-step operation is not used in beginning algebra because there it is classified as unknown. These examples illustrate how MathXpert tailors its output: it sets up an ideal user model based on the initial choice of topic. If the topic is elementary, the user model will set more operations to learning or unknown. If it is advanced, some powerful operations that are not used in elementary topics become available. The original plan [BEES 89] called for the user model to be customized to the individual student and reflect his or her current state of knowledge. It would be updated by MathXpert based on the student's performance, or by the student herself, or by the teacher. However, experimentation with actual students revealed that this was not such a good idea as it first appeared. User models tend to become "unbalanced", and this resulted in awkward solutions, which contained one or two "big" steps mixed with detailed steps. Upon reflection, I realized that when a teacher presents a new topic to a class, he or she lectures to an ideal student who is prepared for this topic by knowing the prerequisite topics, but who does not know this topic yet, or more advanced topics. Thus the final design of MathXpert's user model emerged: it does not model any specific student, but rather an ideal student who is prepared to learn the selected topic. Thus the section title is Instruction is tailored to the student's level, not Instruction is tailored to the student. To see an additional concrete example of how this works, consider the common-denominator problem 1/a + 1/b. In any sufficiently advanced algebra topic, auto mode would change this to (a+b) / ab in one step, with the justification common denominator. But, if the topic selected was Common Denominators, then a five-step solution is generated:
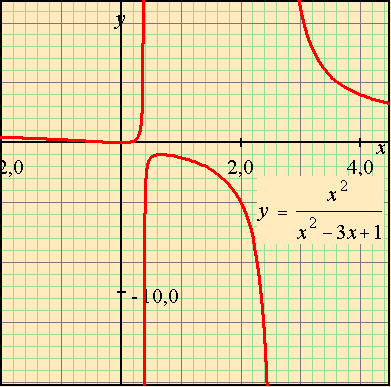
5. MathXpert draws graphs correctly Most other graphing software, including the graphing calculators used in almost every calculus class in the US, draw many graphs incorrectly. This is a result of simply calculating a numerical value of y for each value of x corresponding to a column of pixels and then playing "connect the dots". Several things can go wrong. If the dots cross a singularity of the function, you will get a spurious vertical line. This happens for rational functions and trigonometric functions involving tan x. Some of the graphing calculators have trapped the most common cases, such as tan x itself, but this is an ad hoc measure as tan Öx still exhibits an incorrect vertical line. Textbooks sometimes tell the students that "the calculator draws the asymptotes", but if you graph tan x on a large enough scale, something different goes wrong: the dots on each side of the singularity may still be on-screen, so you don't get vertical lines, but instead just pointy maxima and minima, joined by a line across the singularity. The graph is completely wrong. Similarly, when graphing something like sin(44 x), where the oscillations are packed close together, the graph may miss the maxima and minima, and false maxima and minima appear, in a regular envelope. Again the graph has no relation to reality. Another well-known example (which every teacher types into MathXpert when they try it for the first time) is y = sin( 1/x). Of course, since there is an infinite amount of detail in this graph, it cannot be represented perfectly on a computer screen with finitely many pixels--but MathXpert at least gets it fairly close. MathXpert, unlike any other software, uses its algebraic module and its prover to internally calculate the singularities of a function before graphing it. Here is an example:
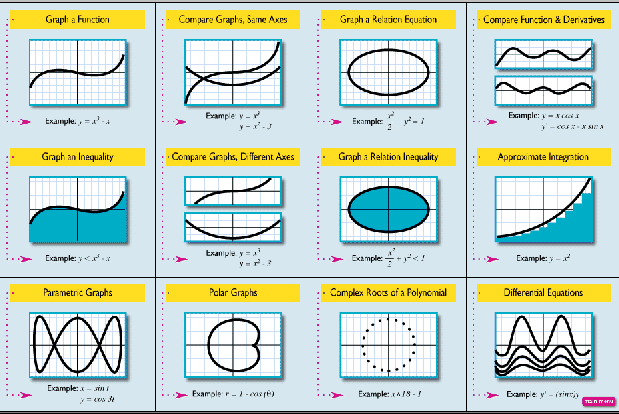
Note that there are no mistaken vertical lines at the singularities, even though the form of the denominator does not make it apparent what the singularities are. You can choose View | Singularities to see the formula MathXpert has calculated for the singularities (not shown here). Of course, it can happen that for a sufficiently complicated formula, MathXpert cannot calculate the singularities. But in that case, the user will get a message to that effect, warning that the graph may be incorrect. You either get a correct graph, or a warning and a (possibly incorrect) graph. It can be proved that it is impossible for any computer program to correctly calculate the singularities of an arbitrary function in the class of functions usually considered in calculus. Given the impossibility of perfection in this respect, MathXpert is rather successful in correctly graphing most functions encountered by students. 6. MathXpert makes it easy to make the graphs students need to see MathXpert can make a wide variety of different kinds of graphs. Variations on the y = f(x) graph include comparing the graphs of two or more functions, either on the same axes or on different axes. You can also graph a relation f(x,y) = g(x,y). You can graph inequalities, either in functional or relational form, and you can graph parametric or polar curves. You can choose which kind of graph you want to make from the following illustrated menu (shown at reduced size):
In all these graphs, you can enter a formula with a parameter (for example, y = sin ax, or y = x3-ax. Then your Graph Toolbar (the row of buttons to the left of the graph) will have buttons that permit you to increase or decrease the value of a, or to access a dialog that permits you to type in a new value of a. The new graphs will be drawn immediately, so with a series of clicks you will see a rapid series of new graphs. You can tell MathXpert to erase the old graphs, or leave them on the screen, as you wish. Other tools on the Graph Toolbar permit you to click to zoom in or out, or to select a rectangle on the visible graph and redraw with that rectangle filling the window. Here is an example of an exercise that could be set by a teacher using the zoom and quick parameter change facilities. The purpose of the exercise is to learn the difference between polynomial and exponential growth. The user chooses Compare graphs (same axes) and enters and xn as the functions. The variable n becomes a parameter and can be increased by a single click. The user increases n until xn appears to dominate 2x. Then, the user zooms the graph a few times, and sees that once again the exponential dominates the polynomial. Increasing the exponent again, the polynomial will dominate on this rectangle. But zooming the rectangle again, the exponential dominates. After this exercise, the student will understand the true relationship between exponential and polynomial growth.
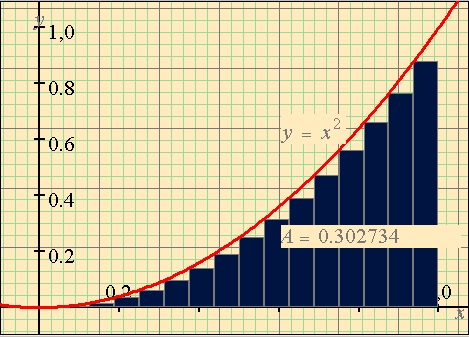
The Point-Slope tool lets you slide a "crosshairs" along the graph, displaying the coordinates and the slope at the crosshair location. Together these tools let you easily explore the graphical meaning of mathematical concepts. Consider the concept of derivative, as the limit of slopes of secant lines. Choosing the topic Compare two graphs (same axes), you can compare the graphs of a function and a secant line, where the secant line has a parameter that can be changed by clicking to make it closer and closer to a tangent. You could even arrange it so that a second parameter controlled the point of tangency. Clicking on the button that increases the parameter, you can show the secant line tending to the tangent. Clicking on the other parameter's buttons, you can move the point along the curve. Using the Point-Slope tool, you can see numerically how the slopes change during this process. The topic of approximate integration is particularly suited to a graphical treatment, and MathXpert makes it very easy to create Riemann sum graphs, and vary the number of intervals with a single click:
It is possible to make Riemann sum graphs using the function value at the left or center of each interval, instead of at the right as shown here. Note that MathXpert also calculates the total area of the rectangles shown, so the student can see how it converges as the number of intervals grows large. The student can click,click,click and watch the number of intervals change. Here the number of intervals has been entered as 2n, so it will double with each click on the button that increments the parameter n. Similar graphs can be made using the trapezoid rule or Simpson's rule. 7.0 How should MathXpert be used? 7.1 MathXpert teaches by example and assistance MathXpert does not provide "lessons" or explicitly tutorial material. Instead, it helps the student do his or her homework. In this sense, it is more like a tutor than a teacher. It does not set the curriculum. The student (or the teacher) poses the problems. (Of course, MathXpert does provide a selection of about 50 problems per topic, and there are about 135 symbolic , that is, non-graphical, topics, so if the student wants MathXpert to supply problems, they are available.) In that context, MathXpert assists the student by preventing mistakes, providing hints, or showing the student how to proceed when he or she is lost. This is exactly what a good tutor should do. As I said in the introduction, MathXpert is designed to replace blackboards and homework, but not teachers and books. It may be possible to learn mathematics from MathXpert without a teacher, but it would require a self-motivated student, and it is not what I am recommending. Instead, I am recommending that teacher and student should both use MathXpert in studying examples of mathematical calculation. Mathematics instruction is structured differently in different countries. The rest of this section draws on the American experience, but I believe that many of the problems that teachers and students encounter in mathematics education are not specific to any country, and I hope that MathXpert will help students and teachers around the world. 7.2 MathXpert supports both traditional and "reformed" curricula Since MathXpert can help the student work on any problem, it can be used with any approach to the subject. The "calculus reform" teachers in the US favor group work and instruction centered around "projects" based on some practical situation. These projects require the use of differentiation, limits, and integration. At the point where these tools of calculus are required, the students can use MathXpert to carry out the necessary calculations. MathXpert works with problems stated in symbols, so if the problem is stated in words, then teacher and students turn to MathXpert only when the problem has been formulated in symbols and calculation is required. At that time, MathXpert can support their learning in the ways discussed above. Conversely, students in a traditional course could simply be given exercises to do in MathXpert. (The teacher can prepare a "problem file" which MathXpert can read, thus relieving the student of having to type the problems in.) 7.3 Using MathXpert outside class--the Estonian experiment One possible approach to using MathXpert is to make it available to students in a computer laboratory (or at home) and just give them access to it to do their homework. This approach requires no change whatsoever to what takes place in the classroom. A controlled experiment has been conducted along these lines in a high school in Estonia. Four sections of calculus were involved. Two of these sections had access to MathXpert after school in a computer lab. The other two sections were denied access. All four sections received the same examinations, lectures, and homework. The results were as follows: the lowest final exam score in the MathXpert sections was 79%. The lowest score in the other sections was 12%, and there were many low scores--as is normal in the course. The MathXpert section scores were abnormal. In the MathXpert sections, every student earned a good score. In other words: in a course where normally lots of students fail, the use of MathXpert brought everyone up to at least B level. Unfortunately, this result could not be published for the following reason: the students were not assigned randomly to the sections. The experimenters just took the sections as they found them. Are you a teacher? Would you like to help replicate this experiment under controlled conditions? Then contact the author of MathXpert at the email address given at the top of this article. 7.4 Using MathXpert's graphics in class I have heard many anecdotal reports of MathXpert being used to project graphs on a screen in high-school classes. The mathematical correctness of the graphs, the facts that they use color and display the formula being graphed, and the ease of zooming or changing a parameter make it ideal for classroom use, far superior to either chalk or a projected graphing calculator. 7.5 Using MathXpert's calculations in class I have personal experience with this, since I taught both trigonometry and calculus using MathXpert during the time when I was developing the program. When I taught trigonometry, the students did not have access to the program themselves, and I used it in class only. It enabled the students to understand very clearly the idea of a step-by-step solution with each line justified. I received homework solutions (done by hand) that looked like MathXpert solutions--beautiful, best-student style solutions. I received these solutions from almost every student. By being repeatedly exposed to menus of applicable mathematical operations, they learned both the specific identities of trigonometry, and the more basic operations of algebra--many of them were quite ignorant of the algebra which was supposedly prerequisite for the course. Even without personal access to the program, mere exposure to it had a noticeable effect. 7.6 Using MathXpert for personalized remediation At my university, all students who wish to enroll for first-semester calculus must take a placement examination. Only after passing this examination may they enroll in calculus--a low score will place them in a "pre-calculus" class. However, the "passing" score is 70%, and the exam itself tests primarily algebra, and is a bit weak on trigonometry. Thus many of the calculus students have large gaps in their algebraic and especially trigonometric knowledge. One semester, I tabulated exam errors and found that 80% of exam errors were due to mistakes in algebra or trigonometry, rather than in the material taught in the calculus course. Traditionally, there is not much a student in this position can do. Such students usually do not have the time or motivation to pursue a systematic study of algebra, and besides, they think that they know it, having already passed the course, often with a good grade. MathXpert offers a clear path for remediation: assign them to spend a few hours solving problems in MathXpert on the specific topics in which they made errors on the placement test. 7.7 Using MathXpert for mass remediation Of course, I am not the first to suggest the use of computers in remedial mathematics. As far as I know, no university has ever been successful in using computers to provide any kind of remedial mathematics instruction routinely to all the students who need remediation. In California, and in the US generally, large numbers of students arrive at the University unprepared in mathematics. Not only that, when these students take remedial classes, there is a large failure rate and as a result, many students are put through the remedial math course a second time. Effective mathematics instruction, supported by time in a computer lab using MathXpert, should thus also prove cost-effective by reducing the repetition rate. My point here is not cost-effectiveness but effectiveness. This method would result in students who really can do mathematics, and whose attitudes towards themselves and towards science and technology would be improved by their successes with MathXpert. Many who otherwise would never be college-educated would succeed, and become productive members of society in jobs that would have not been open to them if they had failed remedial mathematics. 7.8 Teacher training with MathXpert Experience with MathXpert would be beneficial as a regular part of the training for future teachers of mathematics, and also should be useful as an "in-service" workshop (such as teachers take periodically to keep their credential current). In California, some high school math teachers do not have an official credential ("subject authorization") in mathematics. These teachers may be especially interested in MathXpert. Even though I am advocating the use of technology to help with mathematics education, I want to point out the obvious: if we want our students to learn mathematics, the first step should be to provide them all with teachers who know mathematics themselves. 7.9 Using MathXpert with Web-based tutorial material Although MathXpert is designed to replace homework and blackboards, but not teachers and books, interest is repeatedly expressed in a "complete" system, which would provide computer-accessible tutorial material integrated with computer-accessible exercises. There are even voices calling for (or at least predicting) the replacement (or at least the supplementation) of teachers by computerized "intelligent tutors". MathXpert has been engineered to support the creation of Web-based tutorial material by any teacher who desires to create such materials. No skills are required beyond basic computer literacy and of course, the subject knowledge and teaching and writing expertise that would be required to prepare a paper textbook. The student sees a tutorial on a Web page. The page includes pictures of MathXpert graphs and/or calculations, with instructions about what to do with them. For example, the student might be asked to solve a certain equation by adjusting the parameters of a graph in MathXpert, or by carrying out symbolic calculations in MathXpert. When the student clicks on the graph or calculation, MathXpert (on the student's computer) loads that graph for the student to manipulate. When this part of the exercise is completed, the student closes MathXpert and continues the tutorial. Here is a sketch of the process used for preparing such Web pages: The teacher prepares the tutorial Web page in Microsoft Word. The lesson incorporates graphs and calculations from MathXpert. The teacher prepares these graphs and (complete or partial) calculations in MathXpert and saves them, using File|Save. He or she also saves an image of the graph or calculation, using File|Save as bitmap, which is supplied with newer versions of MathXpert just for this purpose. Then the images are pasted into the Word document, and Word's Insert | Hyperlink command is used to create a link to the saved MathXpert file. When Word's Save as HTML command is executed, the images will be converted to .gif files and the entire document will be ready to use. In this sketch I have not discussed the problem of displaying mathematical formulas on a Web page, since that problem is not specific either to tutorials or to MathXpert. Complete instructions, including a solution to the problem of displaying formulas, are available at [BEES 00]. Of course, if the teacher/author is familiar with other tools for Web page preparation, they can be used as well. As soon as one begins to make such tutorials, one wishes that they looked more professional. They need professional graphics, they need animation, etc. The single-author approach described here may be suitable for single-topic tutorials, but just as textbook preparation involves such a team, professional Web publication should also. A team should include a graphic artist, an expert in Web production, and a mathematics teacher. Such a team should be assembled to implement a complete Web-and-MathXpert-based course in algebra. Such a course, in turn, could be of great help in providing remedial instruction that is both effective and affordable. 8. Society and Mathematics Education In this section, I will take up several questions which go beyond the technology of MathXpert and touch on society and its relationships to mathematics and to education. 8.1 The Queen of Sciences will have more courtiers. Mathematics, the "Queen of Sciences", is at the base of the technological pyramid. Physical science rests on mathematics; engineering rests on physical science; and technology rests on engineering. Given the importance of technology in today's world, and the expected increasing importance of technology in the twenty-first century, there is a societal push for more students to learn more mathematics. In California, for example, the governor says that by 2003 every high-school student will have to pass algebra [HSEE 00]. In the past only a small minority of high-school students took and passed algebra. Even without trying to teach all the students, our present efforts to teach algebra are far from completely successful: This year 45 percent of freshmen (first-year students) admitted to the California State University system required remedial mathematics instruction to meet the "entrance-level mathematics" requirements [CSU 00]. In the past, mathematics was taught only to the few who could overcome the difficulties mentioned above. If society intends to teach mathematics to a larger segment of the population, then we are in the position of a space pilot on collision course with a large asteroid: we have a problem. If we can't even teach algebra successfully to those students who are admitted to college, how will we teach it to every high school student? 8.2 Skills versus concepts A solution often suggested in the past two decades is that we should place much more emphasis on teaching the concepts of mathematics, and much less emphasis on computations. This has led to a great deal of controversy, including for example the "California Math Wars" which led to several revisions in the California Mathematics Standards, with the final version being decided upon by the State Legislature, faced with contradictory recommendations. In another example ofthe controversy that has arisen, the United States Department of Education recommended several systems of mathematics education as "exemplary", but two hundred university mathematics professors wrote a public letter of protest and opposition, expressing their opinion that these programs are far from exemplary, and asking the Department of Education to withdraw the recommendations [KLEIN 99]. For example, one of the "exemplary" programs never teaches children how to perform long division. A consultant to the Connecticut Department of Education defended this as follows: "These programs do not teach kids to do five-digit by three-digit long division problems. Instead, they teach all kids, not just a few kids, when and why people need to divide." [COLV 99]. Presumably these students will have calculators in their cell phones, which will always be in their pockets and never out of batteries. The same idea has arisen in various conceptually-oriented systems for teaching algebra and/or calculus, with computer algebra systems replacing the calculator for more advanced computations. There are two separate issues here: It is true that students often do not grasp the concepts underlying mathematics in the sense that they may not recognize when mathematics is applicable to a given situation, or how to analyze a given situation using appropriate mathematics. I do not believe that anyone is opposed to attempts to improve students' abilities to do these things by supplying example situations for them to analyze, possibly in group work as is often advocated. The controversy arises when people want to replace traditional computational instruction with conceptual work. One of the reasons that people make such suggestions is that they want to see students succeeding at mathematics. They want to cut the cycle of frustration leading to reduced motivation leading to reduced effort leading to failure. They think that if they teach concepts instead of calculations, this cycle will be broken. Students will be enthusiastic because they understand, and then they will have increased motivation, will work harder, and succeed more. The point I wish to make on this subject is this: We can have our cake and eat it too, if we make use of MathXpert. Students who use MathXpert to carry out calculations will learn how those computations are done. Because they cannot make mistakes, they will succeed, not fail. Frustration with mathematics will be a thing of the past. If the teacher so desires, the students can use MathXpert in connection with a group project designed to increase their conceptual understanding. But they still will carry out all the steps of the calculations (rather than use a computer algebra system that gives a one-line answer in black-box style). They will learn how to calculate by using MathXpert, while their teachers structure the work so as to teach the desired concepts about how and when to apply mathematics. The vision described in the previous paragraph has to be regarded at present as a pedagogical hypothesis. It should be subjected to a scientific test, to reveal whether it is, or is not, overly optimistic. The claim is in principle testable. 8.3 Mathematics for the masses Lowering the frustration level is the key to teaching mathematics to a greater fraction of the population. How to do that without watering down the curriculum is the question. I respectfully suggest, as the author of MathXpert, that MathXpert might be the answer. In the next section I will spell this out in more detail. Here I spell out the dimensions of the problem.As mentioned above, at the California State University, 45% of incoming freshman are required to take remedial mathematics. (It is now known as "developmental mathematics" to avoid the word "remedial".) A significant fraction of these students require a repetition of the remedial course before they can pass their entry-level mathematics exam. Some never manage to pass it. Starting this year, there is a new rule: they must pass it during their first year at the University, or they will not be allowed to enroll for the second year. Unless present plans change, the University will not even offer remedial courses after 2003, and will no longer accept students who require remediation. It is hoped that this decision will encourage the high schools to do a better job teaching mathematics. If this turns out to be a vain hope, the result will be that the job of remediation will be turned over to California's community college system. These are two-year colleges located in every medium-sized town in California--there are hundreds of these institutions, and they must accept every high school graduate who applies for admission. Supplying remedial mathematics instruction is a major problem in California, and will remain so for the next few years at least, even if the various educational institutions do play "hot potato" with it in an effort to get other institutions to take the responsibility. At the same time, the State of California plans to institute a high school "exit examination" which would have to be passed in order to graduate from high school. The mathematics portion of this examination is described in some detail at [HSEE 01]. The exam is already being admistered, but the class of 2003 is the first that will have to pass it to graduate. This date has already been delayed due to the fear that large numbers of students will fail the mathematics portion of the examination. If this come to pass, the responsibility for remedial mathematics will come to rest on the high schools. Meantime, increased emphasis on standardized testing in the elementary and junior high schools is causing a frenzy of activity and worry about the preparation of students for their high-school mathematics. References [A-K 00] Aleven, V., and Koedinger,K., Limitations of student control: do students know when they need help? in Gauthier, G., Frasson, C., and van Lehn, K. (eds.), Intelligent Tutoring Systems, 5th International Conference, ITS 2000, pp. 292-303, Lecture Notes in Computer Science 1839, Springer-Verlag, Berlin Heidelberg New York (2000). [BEES 89] Beeson, M., The user model in Mathpert: an expert system for learning mathematics, in Bierman, D., Brueker, J., and Sandberg, J. (eds), Artificial Intelligence and Education, pp. 9-14, IOS, Amsterdam (1989). [BEES 92] Beeson, M., Mathpert, Computer support for learning algebra, trigonometry, and calculus, in: A. Voronkov (ed.), Logic Programming and Automated Reasoning, Lecture Notes in Artificial Intelligence 624, Springer-Verlag (1992). [BEES 00] Beeson, M., Making Web pages with Mathpert, http://www.cs.sjsu.edu/faculty/beeson/mathweb/Instructions.html. [CBE 01] California Basic Educational Data System, California Board of Education, http://www.cde.ca.gov/demographic. [COLV 99] Colvin, R., Experts attack math teaching programs, Los Angeles Times, Sept. 17, 1999, page A3. The text is also available at http://mathematicallycorrect.com/experts.htm [CSU 00] California State University, Fall 2000 Regularly Admitted First-Time Freshman Remediation, Campus and Systemwide. http://www.asd.calstate.edu/remediation00. [HSEE 00] California Department of Education, HSEE Mathematics Blueprint, http://www.cde.ca.gov/statetests/hsee/HSEEMathBlueprint.pdf. [KLEIN 99] Klein, D., and 200 co-signers, An open letter to United States Secretary of Education, Richard Riley. Washington Post, Nov. 18, 1999. The text of the letter is available at http://www.mathematicallycorrect.com/riley.htm. [MON 17] Montessori, M., Spontaneous Activity in Education, 1917. Reprinted 1965 by Schocken, New York. |
Help With Math: Purveyors of MathXpert
-->